１ 三坐标测量简介

   三坐标测量机是一种通用性强、自动化程度高 的高精度测量系统。对一般的测量软件而言，三坐标测量机的测量过程，可分为以下几个步骤（假设测头校验与坐标系的建立已经完成）。 

（１）采集特征点的坐标位置。即通过测头直接触测被测对象、 读取并记录坐标值。

（２）按照“最小条件”对前面测得的特征点进行计算与构建。如果是形状误差，可直接计算出误差值。 

（３）如果是位置误差则按照“最小条件”将特征点构建出误差评价所需的点、线、面等基本要素，并用数学的方法计算出各要素间的实际误差，对照图纸判断其是否合格。 在这一过程中，第一步特征点的采集是后续工作的基础，如果有误，构建出的特征要素就不能真实的反映出零件的实际情况，误差计算与评价的结果也就不可信了。因此，特征点的位置、特征点的数量和采集方式对三坐标测量结果有着非常重要的影响。本文就是针对此类问题，对三坐标测量的取点进行了一定程度的实验与讨论，并得出了有益的结论。

２ 平面度测量与评价方法 
   平面度测量是几何量评价的基本内容，是１４类 误差测量（直线度、平面度、圆度、圆柱度、线轮廓度、面轮廓度、平行度、垂直度、倾斜度、同轴度、对称度、位置度、圆跳动、全跳动）中最基本也是最具有代表性的。按照“最小条件”的要求，平面度误差可以由最小包容区域法、对角线法和三点法来评定。以最小包容区域法为例，只要满足了下列条件中的一条，即可确定平面度误差的大小：
（１）三角形法则。图１（ａ）为三角形法则。图中点A为凹形实际表面的最高点，a、b、c为３个最低点，A点的投影落在由a、b、c这３点构成的三角形内。在满足这一条件的基础上，a、b、c点确定平面１，过A点做平面２平行于平面１，则平面１与平面２之间，就构成了最小区域，两平面间的距离即为平面度误差。

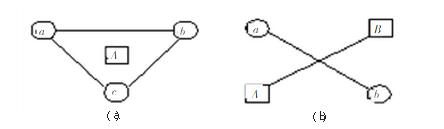
（２）交叉法则。图１（ｂ）为交叉法则。图中点A、点B为鞍形实际面的最高点，点a、点b为最低点，过直线AB和过直线ab决定了一对平行平面，且两直线成交叉状态，则两平行平面就构成了最小区域，两平面间的距离即为平面度误差。
对三坐标测量而言，上述两种评价方式，都是由相应的特征点（最高点和最低点）通过计算得到的，可以这样讲，特征点的位置与数量，实际决定了平面度误差的大小。
另外，评价每一种要素都有一个最低测量点数，如：平面度测量，无论采用哪种法则，都至少要测４点，才能计算平面度误差；直线至少要测３点；圆至少要测４点；圆柱至少要测６点。一般情况下，如果测量条件与对象已经确定，那么测点越多，测得的误差值就越能反映测量对象的真实情况，但考虑到测量效率和经济性，测点不可能无限制的增多，特别是在某些精度与批量都要求比较高的场合，希望能够找到一个合适的测点数，使得测量设备既能较快地完成测量任务，又能较为真实地反映被测对象的实际情况。
3 总结 

三坐标测量机作为一种全新的测量方式，已经 被越来越多的用户所接受和肯定，但由于测量原理的不同，该测量设备有其独特的测量规范。

在三坐标测量中，首先要对特征要素选择合适的测点数，测点数过少，会造成较大的误差；对于确定的测量对象，可以通过样本实验寻找合适的测点数（这对于批量的高精度测量更有意义），以保证测量的精度与效率；比较各类表面，精度高的表面获得的测值，比精度低的表面获得的测值更为可信，测点数对其影响也更小；手动取点误差大，应选用自动测量的方法。采点是三坐标测量的基础工作，为保证测量结果真实可信，应予充分重视。不论是形状误差、还是位置误差，或者尺寸的测量，有了正确的测点信息，才能保证计算评价的真实性。